A Multiscale Finite Element Method Tutorial
This series of tutorials is about different aspects of multiscale finite elements methods. In the first part of it we’re going to meet with some practical aspects of multiscale finite element methods (MsFEM).
So for the sake of simplicity and easy representation of the main ideas, I restrict myself to the model problem:
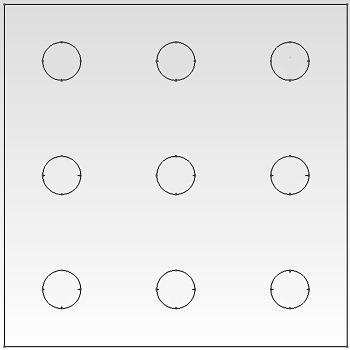
\begin{aligned} \nabla(\lambda(x)\nabla u) &= 0 \mspace{15mu}&&\text{in}\mspace{15mu} &&&\Omega,\\ u &= u_0 \mspace{15mu}&&\text{on}\mspace{15mu}&&&\partial\Omega, \\ \end{aligned}where $\Omega$ is a domain shown in Figure 1 and $\lambda(x)$ is a heterogeneous field varying over multiple scales.
First, I will write a general algorithm of MsFEM:
- 1. Set a coarse mesh configuration (macro-level);
- 2. For each macro-element $ K_j $ of the coarse grid find multiscale basis functions as the solutions of the equations $ \nabla\lambda\nabla\psi_i=0 $ in $ K_j $ with boundary conditions $ \psi_i|_{\partial K_j}=\mu_i $ for each vertex $ i $ (micro-level);
- 3. Using the multiscale basis functions $ \psi_i $ solve the problem on the macro-level.
- 4. On the macro-level and the micro-level we can use different methods to obtain results, so we are not restricted by using only FEM. Also MsFEM is easily parallelized, and it allows to solve problems faster even without parallelization than solving the problems on fine grid.
Now we move to the details. As you may know in FEM instead of solving the problem we solve equivalent equation in Galerkin formulation $ \int_\Omega\lambda\nabla u(x)\nabla v(x)\,d\Omega=0$, where the function $ v(x)$ is a test function. The function $ u$ is represented as $ u=\sum_jq_j\phi_j(x)$, where $ q_j$ are unknown weights and the functions $ \phi_j(x)$ are known basis functions. Then the global matrix is
\begin{equation}\mathbf{A}^{global}\mathbf{q}^{global}=\mathbf{f}^{global} \end{equation} \begin{equation}A_{ij}^{global}=\left\{\begin{array}{c} \sum_{k}\int_{K_k}\lambda\nabla\phi_j^{global}(x)\nabla\psi_i^{global}(x)\,dK_k, i\in N\backslash N_0\\ \delta_{ij}, i\in N_0\\ \end{array} \right. \end{equation}\begin{equation}f_{i}^{global}=\left\{\begin{array}{c} 0, i\in N\backslash N_0\\ u_0(x_i), n\in N_0\\ \end{array} \right., \end{equation}
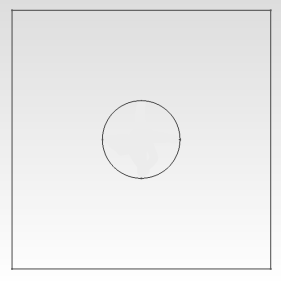
where $ i, j = \overline{1…N}$, $ N$ are global nodes, and $ N_0 $ are nodes on which boundary conditions are set. In MsFEM we should construct the functions $ \psi_i $ that capture the small-scale information within each element. For our problem we build a macro or coarse mesh, so that each macro-element contains one inclusion:

We define $ A_{ij}^{local}=\int_{K_k}\nabla\phi_j(x)\nabla\psi_i(x)\,dK_k$ as a local matrix of a macro-element $ K_k $. We also define four standard bilinear basis functions $ \phi_j $ and four multiscale basis functions $ \psi_i $ in a macro-element $ K_k $.
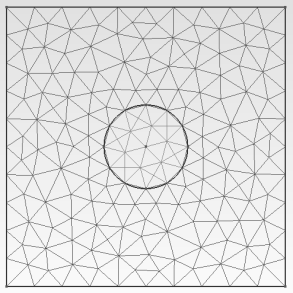
So but how can we construct our four multiscale basis functions in each macro-element? To deal with this we need to solve the following equations for each multiscale basis function:
\begin{aligned} \nabla(\lambda(x)\nabla\psi_i) &= 0 \mspace{15mu}&&\text{in}\mspace{15mu} &&&K_j,\\ \psi_i &= \phi_i \mspace{15mu}&&\text{on}\mspace{15mu}&&&\partial K_j, \\ \end{aligned}where $ i = \overline{1..4}$.
And again we apply FEM to solve it. Thus each multiscale basis function can be represented as $ \psi_i(x)=\sum_{k=1}^{M}q_k^{i, fine}\phi_k^{fine}(x)$, where the functions $ \phi_k^{fine}(x)$ are standard basis functions defined on elements, in our case I use quadratic basis functions in triangles. Then we solve a system of linear equations
\begin{equation}\mathbf{Bq^{i, fine}}=\mathbf{f}\end{equation} \begin{equation}B_{nm}=\left\{\begin{array}{c} \sum_{k}\int_{K_k^{fine}}\lambda(x)\nabla\phi_m^{fine}(x)\nabla\phi_n^{fine}(x)\,dK_k^{fine}, n\in N\backslash N_0\\ \delta_{nm}, n\in N_0\\ \end{array} \right.\end{equation} \begin{equation}f_{n}=\left\{\begin{array}{c} 0, n\in N\backslash N_0\\ \phi_i(x_n), n\in N_0\\ \end{array} \right.\end{equation}where $ n, m$ are global numbers of the fine mesh, $ N_0 $ are nodes on which boundary conditions are set.
Here are the multiscale basis functions for $ \lambda=10^{-3}$ in the circles and $ \lambda=1$ in the domain:
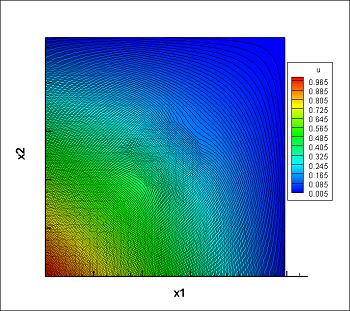
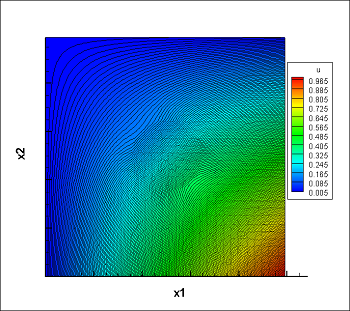
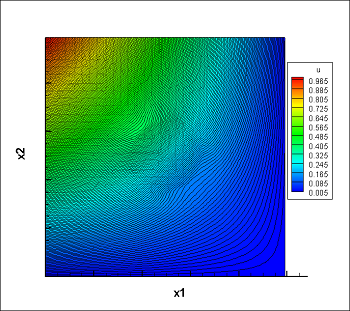
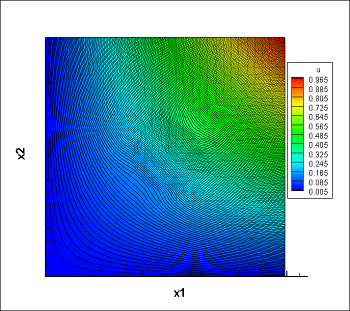
After finding all basis function of each macro-element we can now assemble the local matrices of the macro-level
\begin{equation}A_{ij}^{local}=\int_{K_k}\nabla\phi_j(x)\nabla\psi_i(x)\,dK_k = \int_{K_k}\left(\sum_{k=1}^{M}q_k^{i, fine}\nabla\phi_k^{fine}(x)\right)\nabla\phi_j(x)\,dK_k.\end{equation}Finally, we set boundary conditions to obtain the solution of our model problem. Let $ u=260 $ be on the bottom and $ u=270 $ on the top of the domain.
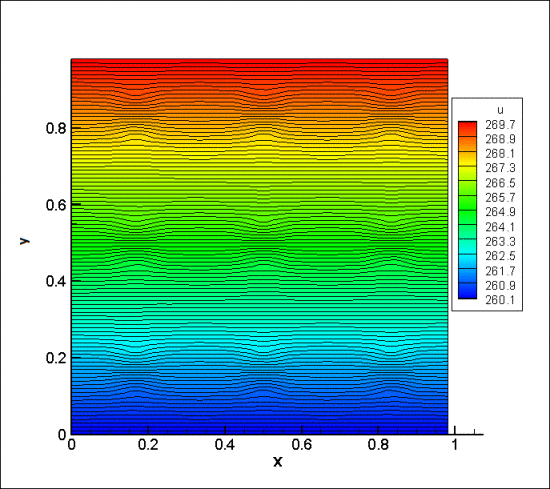
The solution is exactly the same as if we would have obtained it via FEM.
Next time I’m going to show different types of boundary conditions on micro-level called oscillating boundary conditions.
Recommended literature
- Allaire, G. A multiscale finite element method for numerical homogenization / G. Allaire, R. Brizzi // SIAM MMS. – 2005. – 4. – С. 790-812.
- Efendiev Y. Multiscale Finite Element Methods : Theory and Applications / Efendiev Y., Hou T. Y. – B. : Springer, 2009. – 241 с.
- Geuzaine C., Remacle J.-F. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities // International Journal for Numerical Methods in Engineering. 2009. Vol. 79, no. 11. P. 1309–1331.
- Hou. T. Y. A Multiscale Finite Element Method for Elliptic Problems in Composite Materials and Porous Media / Hou. T. Y., X.-H. Wu // Journal of computational physics. – 1997. – 134. – С. 169-189.
- Hou, T. Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients / T. Hou, X.-H. Wu, Z. Cai // Mathematics of Computation. – 1999. – vol. 68 : no. 227. – С. 913-943.