Effective Thermal Coefficients: Analytical Expressions

Before computing the effective thermal coefficients (ETC) in complex media one needs to find the most useful analytical expressions to which one compares obtained numerical results. But why are the ETC needed? So, they are the subject of the homogenization theory that aims at describing the effective (macroscopic) properties of composite materials by means of the characteristics of their micro-structures. As it is known, composite materials are widely used in engineering construction because of their properties that, in general, are better that those of their individual constituents. The homogenization theory covers a wide range of applications ranging from the study of the characteristics of composites to optimal design. Various homogenization techniques are used to predict macroscopic behavior of heterogeneous materials but most of them are not suitable for large deformations and complex loading paths and cannot account for an evolving microstructure and that’s why numerical methods are useful for such purposes.

In this post, I’m going to show you three theoretical models for finding the ETC and their implementation in the programming language C++ 14.

The first of all is the Maxwell model [1]:

\begin{equation}\lambda^*_e=(2+\lambda^*_d-2\xi(1-\lambda_d^*))/(2+\lambda^*_d+\xi(1-\lambda_d^*)),\end{equation}

where $\lambda^*_e=\lambda_e/\lambda_0$, $\lambda^*_d=\lambda_d/\lambda_0$, and $\xi$ is the volume fraction of the inclusions, $\lambda_0, \lambda_d$ are the coefficients of the main material and of the inclusions, respectively.

Bruggeman model [2]:

\begin{equation}\lambda^{*1/3}_e(1-\xi)=(\lambda^*_e-\lambda^*_d)/(1-\lambda^*_d)\end{equation}

Meredith et al. model [3]:

\begin{equation}\lambda^*_e=(2+2x\xi)(2+\xi(2x-1))/(2-x\xi)(2-\xi(x+1)),\\ x=(\lambda^*_d-1)(\lambda_d^*+2).\end{equation}

Source Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <ostream>
#include <fstream>
#include <cmath>
using namespace std;
 
const double Maxwell(const double vol, const double domain, const double in)
{
 const double ld { in / domain };
 const double le { in / domain };
 return (2 + ld - 2 * vol*(1 - ld)) / (2 + ld + vol*(1 - ld));
}
 
const double Bruggeman(const double vol, const double domain, const double in)
{
 const double ld{ in / domain };
 const double le{ in / domain };
 double l{ 1 }, l_pr{ 10 };
 const double eps{ 1e-10 };
 int max_iter = 10000;
 int k = 0;
 while ((fabs(l - l_pr) > eps) && (k < max_iter))
 {
 l_pr = l;
 l = cbrt(l)*(1 - vol)*(1 - ld) + ld;
 ++k;
 }
 return l;
}
 
const double Meredith(const double vol, const double domain, const double in)
{
 const double ld{ in / domain };
 const double le{ in / domain };
 const double x{ (ld - 1) / (ld + 2) };
 return (2 + 2 * x*vol)*(2 + vol*(2 * x - 1)) / ((2 - x*vol)*(2 - vol*(x + 1)));
}
 
void main()
{
 double vol;
 double domain;
 double in;
 ifstream ifs("in.txt");
 ifs >> vol >> domain >> in;
 ifs.close();
 ofstream ofs{ "out.txt" };
 ofs << Maxwell(vol, domain, in) << "\t";
 ofs << Bruggeman(vol, domain, in) << "\t";
 ofs << Meredith(vol, domain, in) << endl;
 ofs.close();
}

Results

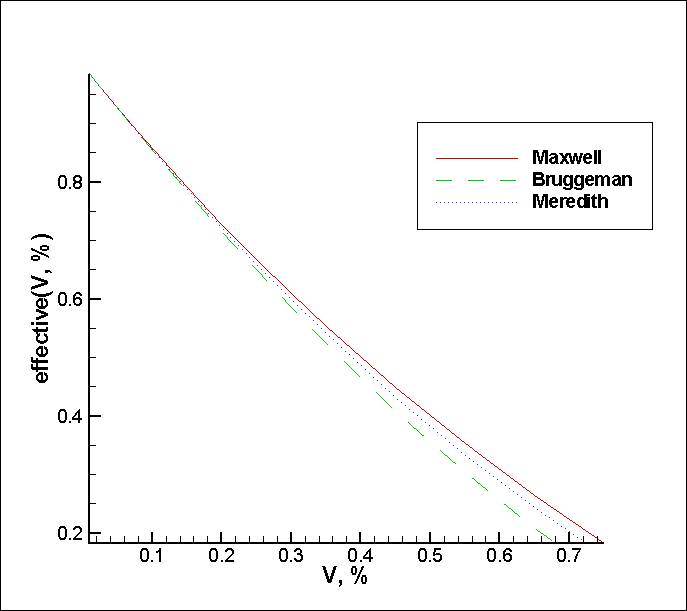
So, here’s the results of the calculations for two different concentrations $\lambda_0=1, \lambda_d=1\mathrm{e}{-3}$.

Bibliography

[1] J.C. Maxwell, A treatise on electricity and magnetism, 3rd Ed., Clarendon Press, Oxford, 1881.
[2] D.A.G. Bruggeman, Berechnung verschiedener physikalisher konstanten von heterogenen substanzen, Ann. Physik., 24 (1935), 636-664.
[3] R.E. Meredith, C.W. Tobias, Conductivity of Emulsions, J.Electroch. Soc. 103 (1961), 286.